
Note: most of the information on this page is pre-2008. Pomacea bridgesii is now considered a synonym for P. diffusa, although P. bridgesii is still the primary name used here.
Set theory works fairly well for predicting the inheritance of various pigment expression traits in Pomacea bridgesii. The model assumes that all Pomacea bridgesii traits are simple Mendelian traits, meaning that there are only two forms of any given trait (no allowances for incomplete dominance or codominance). Of course, as these snails were selectively bred over time, it became clear that the model is not perfect and that there are some subtleties in the colors that remain without a good explanation, such as why one snail will be a very bold yellow while another is very pale. Some of this variation is likely environmental. Still, the simple mendelian model proposed here has worked pretty well over time. This model also only gives supersets of possibilities, which is to say more combinations than what is likely to happen in reality, and there are no associated probabilities with the outcomes.
Set Theory Introduction
A set is a group of objects. Each object must be unique, and there is no order of importance among the objects. An object in a set is called an element. A set is denoted using {} brackets and commas between each element. A set can be assigned a letter or name to identify it. For example, the following set has five elements: S={1,2,3,5,7}.
As with numbers, there are several operations that can be performed on one or more sets. The union of two sets is the set of all elments of the first set, along with all the elements from the second set that are not in the first set (because there can be no repeated elements). For instance, the union of the set S defined above and the set A={2,4} is: {1,2,3,4,5,7}. The union operation is important for this model of color trait inheritance in Pomacea bridgesii.
A subset of a set is a set of elements contained within the parent set. For example, the set {1,2,3} is a subset of the set S defined above.
Another important set operation for this model is the formation of a power set. A power set is a function of another set that produces the set of all subsets of that set. The power set of the set B={1,2,3} is:
P(B) = { {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}, {null} }
For the purpose of this model, each element represents the expression of one pigment trait. Each set represents a group of potential traits to be passed on, either from a specific individual or from a combination of two individuals. The presence of an element indicates the expression of a trait, and the absence of an element indicates that the trait is not expressed. Each letter represents a trait element as follows:
- S – expression of the stripe pattern on the shell
- B – expression of pigment in the shell base
- D – expression of dark pigment in the body
- Y – ability to produce yellow pigment
- M – ability to produce magenta pigment
- C – ability to produce “cyan” pigment (closer to teal in reality)
- P – expression of yellow pigment in the shell base
- Q – expression of magenta pigment in the shell base
- R – expression of “cyan” pigment in the shell base
A snail’s traits should be considered as though the snail was “constructed” starting from a plain white/ivory snail with no dominant traits. So, a golden snail has the following traits: {B,Y,P}. A plain ivory snail with no dominant traits is represented as the null set: {null}, indicating no expression of pigment traits. However, it should noted that although that is one genetic combination that can produce an ivory snail, other combinations can, in reality, result in an ivory snail that is carying some dominant traits, namely: {P,Q,R} (ability to put all pigments in the shell base, but pigment production overall in the shell is turned off), {Y,M,C} (ability to produce all pigments, but all expression locations turned off). All subsets of either {P,Q,R} or {Y,M,C} produce ivory snails. This indicates that there is some presidence in the traits; primarily:
- Lack of B overrides presence of P,Q, and R. If B is turned off (not in the set), no pigment is expressed in the shell base, despite ability to produce pigments.
- Lack of S and B in the same genetic set overrides presence of P, Q, R, Y, M, and C. Pigment expression localities are turned off.
- For the shell base: lack of P overrides Y, lack of Q overrides M, lack of R overrides R.
Those rules as well as others are implied by the definition of the letters/genes.
Building the set of genes for a snail can be tricky, since there are multiple combinations for each color. To maximize the number of possible outcomes for a given color cross, always include Y, M, C, Q, R, and S where it will not change the color of the parent snail.
Method for Predicting Color Trait Inheritance
1.Build the gene sets for BOTH parents according to the guidelines above (for simplicity called A and B). If the whole gene set is not clear (as for the case of an ivory snail), you can either maximize the possible results as described above or minimize the results by removing those same key letters where it will not affect the overall color of the parent snail.
2. Find the union of the sets from both parents (A unnion B). DO NOT INCLUDE DUPLICATE ENTRIES. In this case, {X,Y} is the same as {Y,X}. If S is a trait for both parents, the union set should have only one element that is S. The same applies to all traits.
3. Find the power set of A union B: P(A union B) = {power set}. BE SURE TO INCLUDE THE NULL SET AS ITS OWN ELEMENT. This set of subsets will be all possible trait combinations that the offspring can have.
<b>An Example</b>
Parent 1 = golden
Parent 2 = ivory, known to carry the stripes trait
Offspring will be minimized for simplicities sake.
Ivory genotype: A = {S}
Golden genotype: B = {B,Y,Q}
Union operation = "U"
A U B = {S,B,Y,Q}
P(A U B) = { {S}, {B}, {Y}, {Q}, {S,B}, {S,Y}, {S,Q}, {B,Y}, {B,Q}, {Y,Q}, {S,B,Y},
{S,B,Q}, {S,Y,Q}, {B,Y,Q}, {S,B,Y,Q}, {null} }
Offspring color analyses (determining the color of each subset):
S = ivory
B = ivory
Y = ivory
Q = ivory
S,B = ivory
S,Y = gold striped ivory
S,Q = ivory
B,Y = ivory
B,Q = ivory
Y,Q = ivory
S,B,Y = gold striped ivory
S,B,Q = ivory
S,Y,Q = gold striped ivory
B,Y,Q = golden (not striped)
S,B,Y,Q = gold striped golden
Note that this method is NOT an indicator of probability. The number of occurances of a color
in the offspring power set is not useful for predicting the percentage of a color yield. It
is genearlly more accurate to assume that the probability of color yield will be from greatest
for the most dominant-carrying parent's color with falling probability of colors containing
progressively less dominant traits.
Phenotype examples
Light burgundy (reddish brown base, stripes, and light foot):
Olive (greenish base, darker stripes, and dark foot):

Blue (pigmentless shell, dark foot):
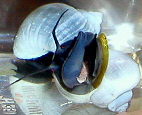

Blue-green purple. Teal base, purple stripes, dark body. Shown with bright and dim lighting.


Dark striped purple (purple base, purple stripes, dark foot even though the flash makes it look weird)

Striped golden (yellow stripes, yellow base, white foot):

Jade (yellow shell, no stripes, dark body)

Striped purple (pink/purple base, purple stripes, light body)

Light striped purple (clear/white base, purple stripes, light body)

Clear base, brown stripes, light body:

Striped purple (purple base, very wide purple stripes, light body):

Solid purple (no stripes, purple base, light body):

Wild (brown base, black-brown stripes, dark body):



